A fibration model for $d$-dimensional image patches

Brad Nelson

Department of Statistics & CCAM

University of Chicago

AMS Special Session on Applied Topology
January 8, 2021
bnels.github.io/jmm2021

Acknowledgement/Support

Thanks to Gunnar Carlsson for many discussions on the Klein bottle for image patches and possible extensions.

Funding I received while working on this topic

• DoD through NDSEG fellowship
• DOE through SLAC/Neutrino group
• Unbox AI

Outline

1. Image Patch Data
2. Data Exploration
3. Fibration Model
4. Fibration-Assisted Visualization

Image Patch Data

2D: $\ell \times \ell$ pixel squares.

3D: $\ell \times \ell \times \ell$ voxel cubes.

Patches are sampled from natural (non-random) images, so there is structure in the data.

Filter for high-contrast, dense subsets.
k, p: take top p% ranked by distance to k-nearest neighbor.

Topology of Image Patches

• [LPM 02] find annulus when investigating patch statistics
• Preliminary topological investigations in [dSC 04]
• Klein bottle model proposed in [C+ 08]
• Compression [MSC 08] Texture recognition [PC 14] Neural nets [GC 19]
• Range images [AC 09] Flow [A+ 20]

Topology in the visual cortex

• [T 95] Klein bottle model in stimulus maps.

Klein Bottle In Image Patches

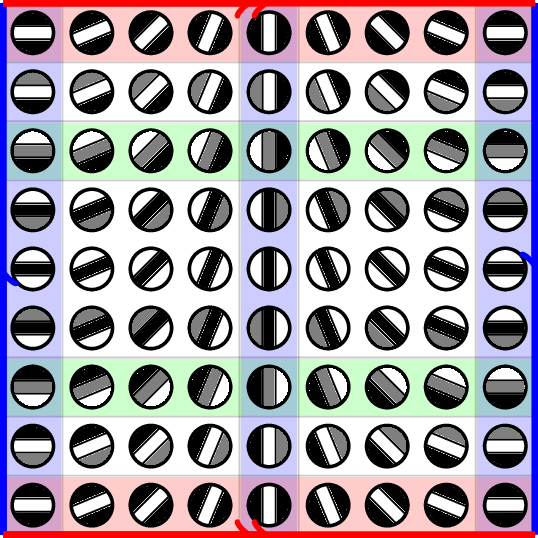
Contributions

• Topological modeling of 3D image patch data.
• Analyze a fiber bundle model that generalizes Klein bottle for 2D patches.
• Use this to understand the distribution of patches in different data sets.

Data

Van Hateren data set [vHvdS 98] - data base of 2D natural images.

BRATS MRI data set [BRATS]

Penobscot seismic interpetation data [Pen]

Data Processing

Procedure used in [LPM 02]

1. Sample random patches
2. Take top 20% by contrast norm
3. Mean-center and normalize contrast

Additional steps used for high-density regions [dSC 04, C+ 08]

1. Compute distances to $k$-nearest neighbor
2. Take $p$% by smallest distance

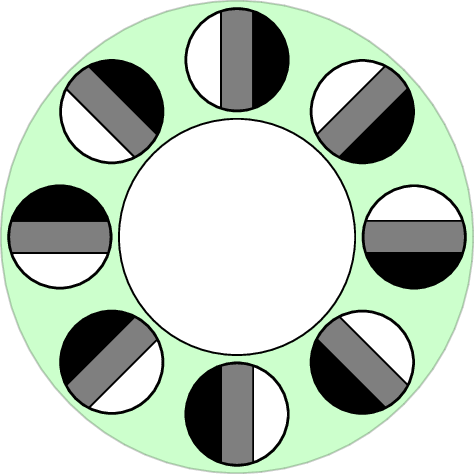
Van Hateren, k=100 p=20

2-dimensional PCA embedding with eigenpatches.

$7\times 7$ patches
Primary circle [dSC 04]

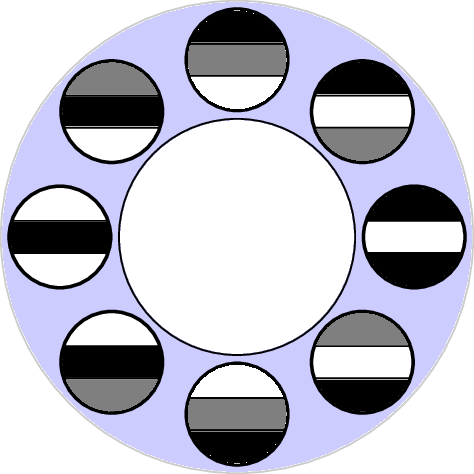
Penobscot, k=30 p=40

2-dimensional PCA embedding with eigenpatches.

PCA 1

$5\times 5\times 5$ patches

PCA 2

BRATS k=100 p=40

The model space $\cal K^d$

Consider $d$-dimensional patches.
We'll consider idealized patches as functions on the disk $D^d$
We'd like to capture primary spheres and secondary circles in a topological model.

The primary $(d-1)$ sphere [dSC 04]:
$\{(v_\phi^T x) \mid v_\phi\in S^{d-1}\}$

The model space $\cal K^d$

Fix $v_\phi \in S^{d-1}$. A secondary circle [dSC 04]:
$\{\cos(\theta)(v_\phi^T x)^2 + \sin(\theta)(v_\phi^T x)\mid \theta \in [0,2\pi)\}$

Note that $v_\phi$ and $-v_\phi$ produce the same secondary circle.

The model space $\cal K^d$

$\mathcal{K}^d = \{ k(v_\phi, \theta; x) = \cos(\theta)(v_\phi^T x)^2 + \sin(\theta)(v_\phi^T x) \mid v_\phi\in S^{d-1}, \theta \in [0,2\pi) \}$
There is an identification $k(-v_\phi, -\theta;x) = k(v_\phi, \theta; x)$

$\mathcal{K}^2$ is a Klein bottle [C+ 08]. $\mathcal{K}^3$ is a $3$-dimensional manifold.

The Harris Map

Harris corner/edge detector [HS 88] analyzes eigenvalues of:
$M(x) = \sum_i \Delta(x_i) \Delta(x_i)^T$, $\Delta$ finite difference gradient.
Harris map $h: x\mapsto \text{MaxEigVec}(M(x))$

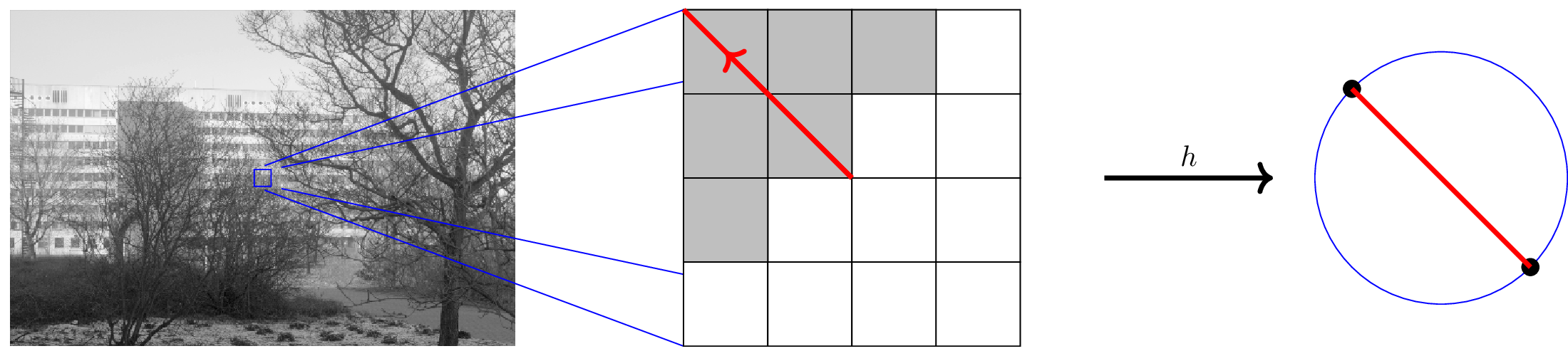
There is a sign/scale ambiguity for eigenvectors, so range is naturally $\mathbb{R}P^{d-1}$
We also see this ambiguity in our "secondary circles".

The Harris Map

Continuous limit
$M(f(x)) = \int_x dx\, \nabla(f(x))\nabla(f(x))^T$
For $k(v_\phi, \theta; x)\in \mathcal{K}^d$, $\nabla(k(x)) = k'(x) v_\phi$
so $M(k(x))$ is rank-1, and $h(k(v_\phi, \theta; x)) = [v_\phi]$

$\mathcal{K}^d$ is a fiber bundle over $\mathbb{R}P^{d-1}$
(non-trivial because of twist in identification)
The Harris map $h$ is a fibration for $\mathcal{K}^d$
Fibers $h^{-1}([v])$ are secondary circles.

Homology of $\cal K^d$

Because of fibration structure, we can use Leray-Serre spectral sequence to compute homology.
We'll use integer ($\mathbb{Z}$) coefficients, which can be used to obtain field coefficients.

$H_\ast(\mathcal{K}^2) = (\mathbb{Z}, \mathbb{Z}\oplus \mathbb{Z}_2, 0)$
$H_\ast(\mathcal{K}^3) = (\mathbb{Z}, \mathbb{Z}_2\oplus \mathbb{Z}_2, 0, \mathbb{Z})$

See [N 20] Theorem 5.2.6 for detailed calculations.

Fibration-Assisted Visualization

3D patches are high dimensional (125 dimensions for 5x5x5).
PCA can visualize some simple structures.
$\mathcal{K}^3$ is a 3-dimensional manifold that captures more.

Visualize data using affine space of $\mathcal{K}^3$

• $xy$-plane: Stereographic projection of $\mathbb{R}P^2$ base space
• $z$-axis: $S^1$ fiber cut at $2\pi$

BRATS patches on $\cal K^3$

xy axis is stereographic projection from 3rd spherical coordinate

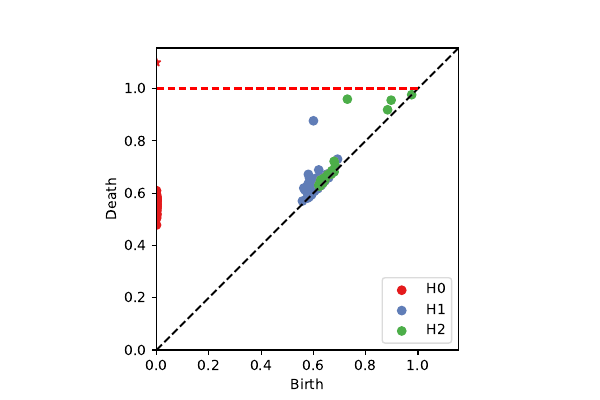k=100, p=40: 2-sphere + circle (chord) 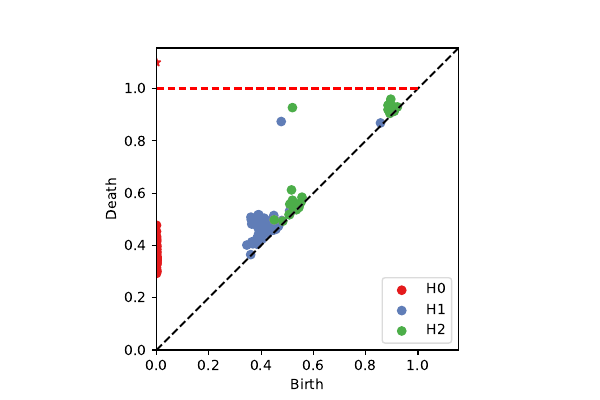projection onto $\mathcal{K}^3$

Penobscot patches on $\cal K^3$

xy axis is stereographic projection from 2nd spherical coordinate

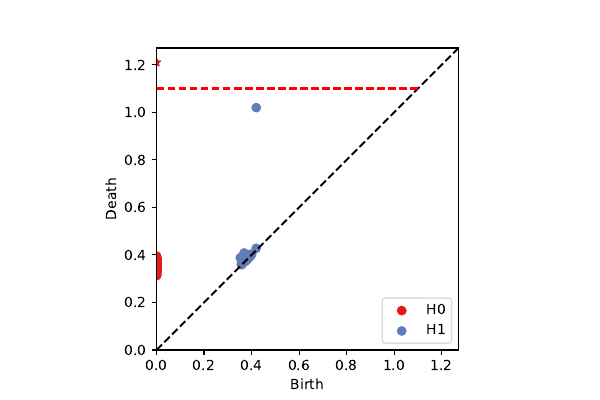k=100, p=40: secondary circle 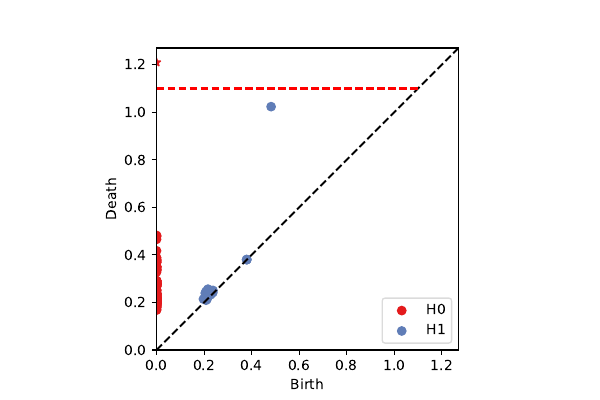projection onto $\mathcal{K}^3$

Review & Future Directions

We've developed a model $\cal K^d$ to explain structures we see in image patch data.

• Useful for interpreting subsets of the data.
• Captures topology of high-dimensional data with small number of dimensions.

For additional details, see [N 20] "Parameterized Topological Data Analysis."

Potential applications: 3D compression, texture, neural nets [MSC 08, PC 14, GC 19]

If we have higher-dimensional patches, we could perform similar analyses.
Where would a 4-dimensional image come from?

Other applications where we might use a map:
Evasion [AC 14], Time series, Control systems.

Technical Credits

• Slides made with reveal.js
• Topological computations done with BATS and BATS.py
• Interactive visualizations made with plotly

Bibliography

[N 20] B. Nelson. Parameterized Topological Data Analysis.
PhD Dissertation, Stanford University. 2020. (Link)