Parameterized Topological Data Analysis
Brad Nelson
Institute for Computational and Mathematical Engineering
Stanford University
May 5, 2020
bnels.github.io/phd-talk
Collaborators/Support
Collaborators who appear in this work
- Gunnar Carlsson
- Anjan Dwaraknath
Funding I've received while working on these topics
- DoD through NDSEG fellowship
- DOE through SLAC/Neutrino group
- Unbox AI
Outline
- Introduction to Topological Data Analysis (TDA).
- Matrix factorization algorithms and quiver representations for TDA.
- Parametrization with cover complexes.
- The topology of 3-dimensional image patches.
Topological Data Analysis (TDA)
Concerned with understanding and using data through topology.
Data sets as topological spaces. Data points as topological spaces.
Compute algebraic signatures of shapes.
Application of homology to data begun by Robins [R 00],
furthered by [ELZ 02], [ZC 05], [CdS 10].
Applications (necessarily incomplete list):
Data visualization (mapper) [SMC 07], neuroscience [GGB 16], molecular properties [CWD 17], materials discovery [H+ 16], regularization [GND+ 20], genetics [CGR 13]
Topological Features
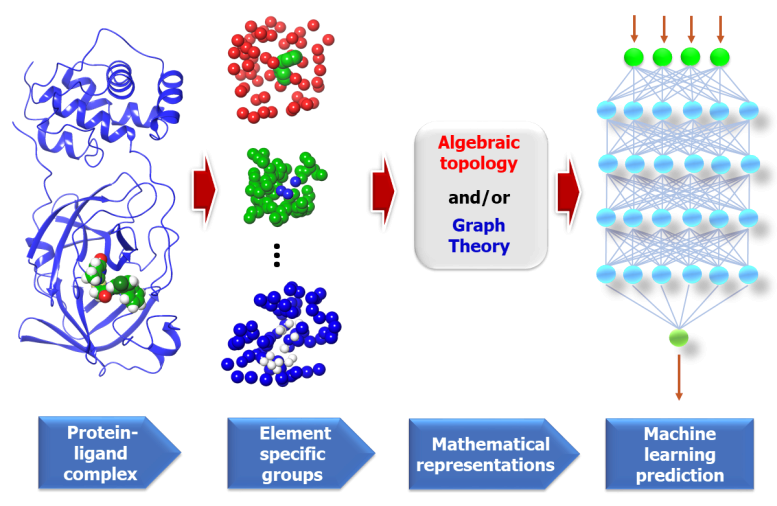
Figure from "Potentially highly potent drugs for 2019-nCoV" Nguyen et al. [N+ 20]
Topology of Data Sets

Topology in Image Patches
Algebraic Topology Review
Data set (discrete topological space) $X$.
$k$-simplex $(x_0,\dots,x_k)$ is the span of $k+1$ points in $X$.
Simplicial complex (topological space) $\mathcal{X}$ built from simplices.
Chain complex $C_\ast(\mathcal{X})$ (assume field coefficients).
$C_k(\mathcal{X})$ vector space with basis vector for every $k$-simplex.
Differential maps $\partial_k: C_k(\mathcal{X}) \to C_{k-1}(\mathcal{X})$, $\partial_k \circ \partial_{k+1} = 0$.
Homology $H_k(\mathcal{X}) = \ker \partial_k / \text{img} \partial_{k+1}$ quotient vector space.
$\dim H_0(\mathcal{X})$ = # connected components, $\dim H_1(\mathcal{X})$ = # of loops, ...
Maps $f:\mathcal{X}\to \mathcal{Y}$ produce induced maps $H_k(f) : H_k(\mathcal{X}) \to H_k(\mathcal{Y})$
Homotopy invariance: if $\mathcal{X}\simeq \mathcal{Y}$, $H_\ast(\mathcal{X}) \cong H_\ast(\mathcal{Y})$.
Persistent and Zigzag Homology
Persistent homology [ELZ 02]
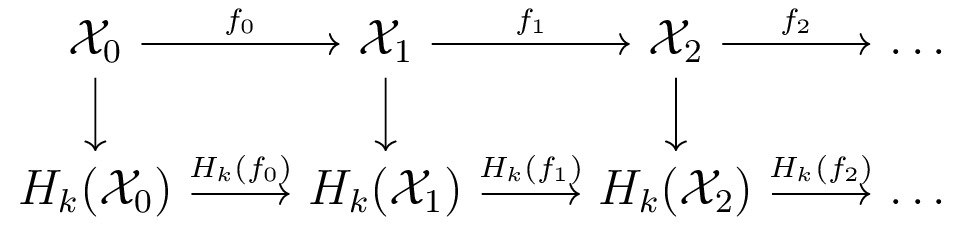
Zigzag homology [CdS 10]
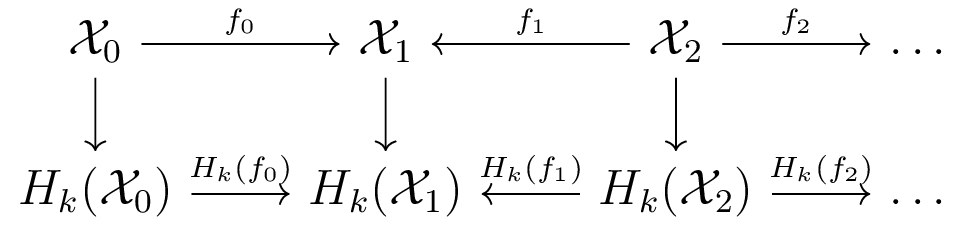
Barcodes track how homology is created and destroyed.
Parameterized TDA
Classical topology:
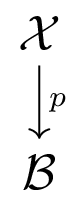
$\mathcal{B}$ called base space. Study $\mathcal{X}$ through fibers $p^{-1}(b)$ parameterized by $b\in \mathcal{B}$.
Data is typically discrete. Sometimes more sensible to talk about covers $\mathcal{U}$, and pullbacks of covers $p^{-1}(\mathcal{U})$.
Why? Lots of structure to use - gives more ways to compare different data.
Can we bring computational tools (long exact and spectral sequences) to setting of data?
Topological Simplification
Simplicial complexes often contain much more information than is needed.
This can make computations much more expensive than necessary.
One idea is to use a cover $\mathcal{U}$ of $X$, and use the nerve $\mathcal{N}(\mathcal{U})$.
Nerve Theorem [B 48] (informal): For nice $\mathcal{U}$ and nice $X$, $\mathcal{N}(\mathcal{U}) \simeq X$.
Unfortunately, this isn't immediately useful for discrete data.
Computing Zigzag Homology
How can we compare two (or more) covers?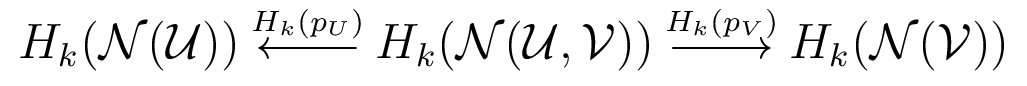
We'll call $\cal N(\cal U, \cal V)$ the bivariate nerve.
Something like this proposed in [CdS 10] for Witness Complexes
Prior Work on Zigzag Homology
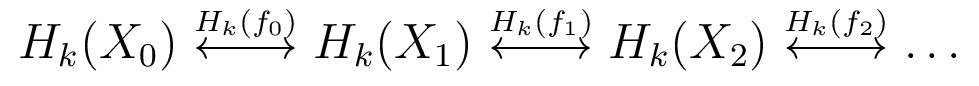 Note: persistent homology is special case
Note: persistent homology is special case
- Zigzag homology introduced by [CdS 10]
- Algorithm for special case of inclusions [CdSM 09]
- Only widely available implementation in Dionysus [M]
- Work on applications to Rips complexes [OS 15]
- Examples of type-A quiver representations [G 72]
No computational tools for bivariate Nerve diagram
(maps are not inclusions)
Contributions
- New computational framework for computing persistent and zigzag homology
- Handles arbitrary maps between spaces
- Multiple opportunities for parallelization
We can compute zigzag homology of bivariate nerve diagrams!
Persistent and Zigzag Homology: A Matrix Factorization Viewpoint [CDN 19]
Code: BATS and BATS.py
See also Anjan's forthcoming thesis [D 20].
Parallelization of Homology Functor
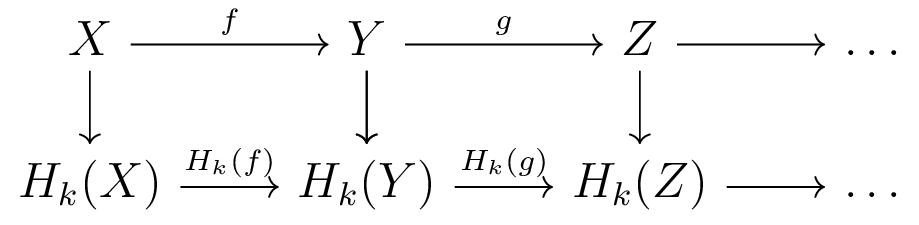
- Computing Homology of each space embarassingly parallel
- Computing each induced map embarassingly parallel
Existing TDA packages work on chain complexes
(Makes sense if all maps are inclusions)
We take advantage of this parallelization.
Quiver Representations
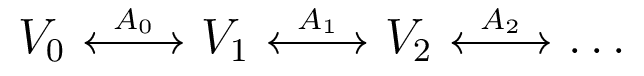
- Diagram of vector spaces, linear transformations
- type-A quiver representations are on a line graph
- [G 72]: type-A quiver representations have finite indecomposables
- [CdS 10]: barcodes are the indecomposable forms
Example: Indecomposable for bar with birth at 1, death at 2:
$I[1,2] = 0 \leftrightarrow \mathbb{F} \overset{\cong}\leftrightarrow \mathbb{F} \leftrightarrow 0 \leftrightarrow \dots$
Type-A quiver representations are isomorphic to something in the form
$\bigoplus_i I[b_i, d_i]$
The Companion Matrix
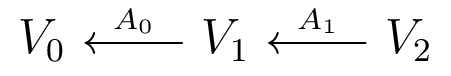
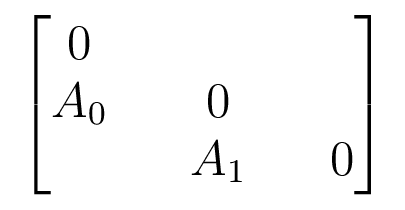

Acts on $V_0 \oplus V_1 \oplus V_2$
The Barcode Factorization

$E_i$ have at most 1 nonzero in each row and column
Can read barcode off from $\Lambda$ by tracking basis vectors
[CDN 19]: the barcode form $\Lambda$ doesn't depend on choice of basis in each vector space
Further Details
- Reversed arrows use $PU\hat{E}_L L$ factorization instead (zigzag)
- Can start at other end of diagram using $PLE_U U$ factorizations
- Combine to get divide-and-conquer scheme to parallelize
Review and Future Directions
- New computational framework for persistent/zigzag homology.
- Can be applied to any maps.
- New applications.
Future directions:
- Quiver representations other than type-A?
- Combine with other optimizations for persistent homology.
Cover Complexes
Rips filtrations $\mathcal{R}(X; r)$ are expensive to use.
Difficult to compute high dimensional homology in most situations. True for other constructions as well.
To compute $PH_3(\mathcal{R}(X; r))$ when $X$ has 1000 points, need $\binom{1000}{5}$, about 10 trillion, 4-simplices.
May need even more than 1000 samples to resolve interesting structure.
Prior Work
[S 13] Linear-size approximations to Rips complex.
Constant factor may be large.
[GS 17, CS 18] Approximations using filtered Nerves.
Focus is on when Nerve is good approximation.
[LM 15] Mayer Vietoris spectral sequence
[Y 18] Leray spectral sequence + sheaf cohomology
Cover Complexes
We'll analyze the cover filtrations $\mathcal{X}(\mathcal{U}; r)$.
Idea: restrict simplices in a filtration $\mathcal{X}(r)$ to open sets in $\mathcal{U}$.
If we cover 1000 points with 40 overlapping sets of 50 points each, get
$\le 40 \binom{50}{5}$, or about 100 million 4-simplices (instead of 10 trillion).
- New method of constructing complexes from point cloud data using a cover.
- Reduce the size of geometric complexes.
- Understanding of how this relates to different constructions.
Implementations available in BATS.
Comparison using Interleavings
We can compare $PH_k(\mathcal{X}(t))$ and $PH_k(\mathcal{Y}(s))$ using an interleaving
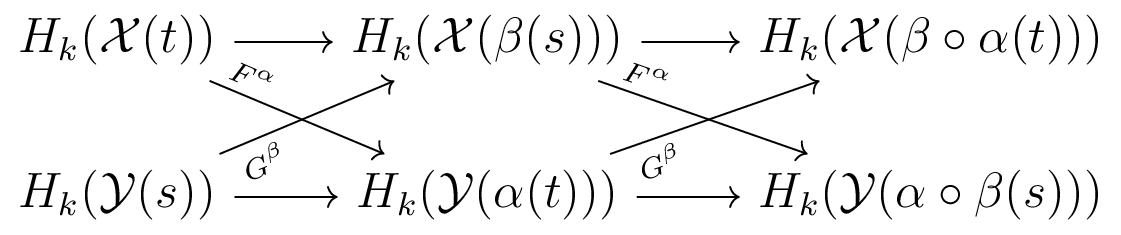
In this case, we say $PH_k(\mathcal{X}(t))$ and $PH_k(\mathcal{Y}(s))$ are $(\alpha,\beta)$-interleaved.
Equivalent to the bottleneck distance on persistence diagrams [L 15].
How to Construct Maps?
In general can be difficult to write down "by hand".
Acyclic carrier theorem [M 80] can be used to
algorithmically generate maps from initial data (easier).
[N 20] extends the acyclic carrier theorem to filtrations.
Basic idea: carrier $\mathscr{C}$ assigns simplices in $\mathcal{X}$ to sub-complexes of $\mathcal{Y}$.
We can always generate maps when these subcomplexes satisfy acyclic condition.
$\ker \partial_k = \text{img}\, \partial_{k+1} \Rightarrow H_k = 0$, or contractible.
A Nerve Theorem
Let $\bar{\mathcal{U}}$ denote the collection of all non-empty intersections of sets in $\mathcal{U}$.
[N 20] (Informal) Suppose $PH_\ast(\mathcal{X}(U; r))$ is interleaved with something acyclic for all $U\in \bar{\mathcal{U}}$. Then $PH_\ast(\mathcal{X}(\mathcal{U}; r))$ and $PH_\ast(\mathcal{N}(\mathcal{U}))$ are also interleaved.
Specialization of results in [GS 17, CS 18]Stability
If points in $X$ are perturbed, how does $\mathcal{R}(X,\mathcal{U};r)$ change?
[N 20] (Informal) Let $X,Y$ be samples, and $\mathcal{U}$ a cover of $X\sqcup Y$. If all the sets in $\bar{\mathcal{U}}$ restricted to $X$ are close (in Hausdorff distance) to the sets restricted to $Y$, then the cover complexes have close persistent homology.
$\mathcal{R}(X, \mathcal{U}; r)$ vs. $\mathcal{R}(X; r)$
Different regimes [N 20]:
- For some $R \ge 0$, $\mathcal{R}(X, \mathcal{U}; r) = \mathcal{R}(X; r)$ for $r\le R$.
- For some $R' \ge 0$, $\mathcal{R}(X, \mathcal{U}; r)$ and $\mathcal{R}(X; r)$ are not interleaved for $r\ge R'$, unless $\mathcal{N}(\mathcal{U})$ is contractible.
- Intermediate regime where $\mathcal{R}(X, \mathcal{U}; r)$ and $\mathcal{R}(X; r)$ are non-trivially interleaved.
Example
Flat torus sampled on $20 \times 10$ grid (200 points).
Cover pulled back from cover of 1st circular coordinate.
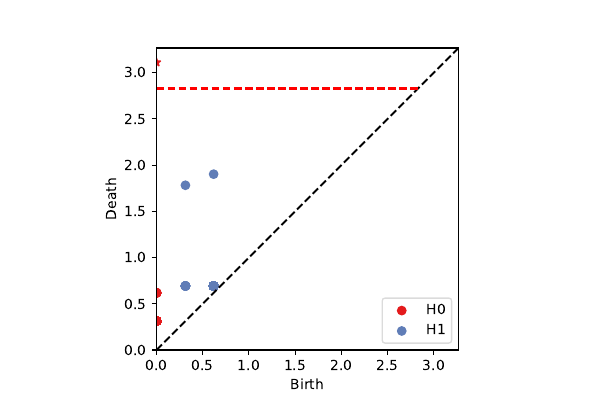
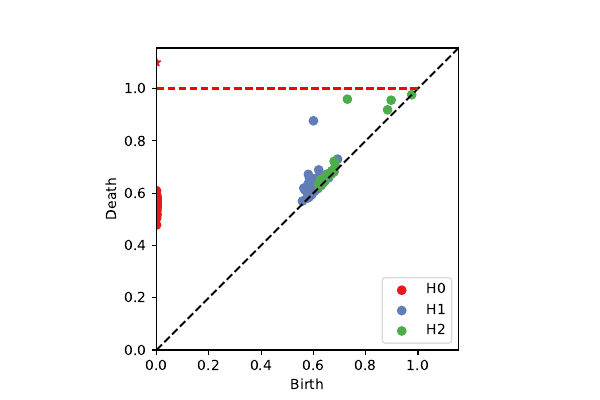
Rips Filtration
1,333,500 simplices
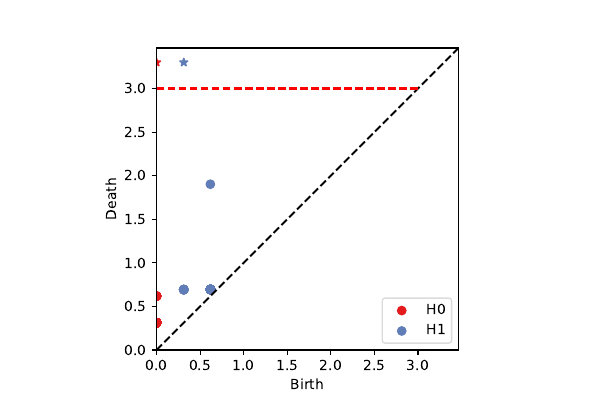
Rips Cover Filtration
23,500 simplices
Review and Future Directions
- Cover complexes can drastically reduce the size of geometric complexes.
- Filtered version of acylic carrier theorem for constructing interleavings.
- We've seen how this compares to the "full" complex for Rips construction.
Future directions:
- Cover complexes fix geometry of cover. Use this in ML pipelines?
- Amenable to parallelization. Adapt scheme from [Y 18]?
- Algorithmic applications of filtered acyclic carrier theorem?
The Topology of Image Patches
2D images: $\ell \times \ell$ pixel squares sampled from images.
3D images: sample $\ell \times \ell \times \ell$ voxel cubes.
Patches are sampled from natural (non-random) images, so there is structure in the data.
Filter for high-contrast, dense subsets of data.
k, p: take top p% ranked by distance to k-nearest neighbor.

Prior work
Contributions
- Topological modeling of 3D image patch data.
- Analyze a fiber bundle model that generalizes klein bottle for 2D patches.
- Use this to understand the distribution of patches in different data sets.
Data
Van Hateren data set [vHvdS 98] - data base of 2D natural images.
BRATS MRI data set [BRATS]
Penobscot seismic interpetation data [Pen]


Van Hateren, k=100 p=20
2-dimensional PCA embedding with eigenpatches.



$7\times 7$ patches
Primary circle [dSC 04]
Penobscot, k=30 p=40
2-dimensional PCA embedding with eigenpatches.

$5\times 5\times 5$ patches
BRATS k=100 p=40
3-dimensional PCA embedding with eigenpatches.PCA 1
$5\times 5\times 5$ patches
PCA 2
The model space $\cal K^d$
Consider $d$-dimensional patches.
We'll consider idealized patches as functions on the disk $D^d$
We'd like to capture primary spheres and secondary circles in a topological model.

The primary $(d-1)$ sphere:
$\{(v_\phi^T x) \mid v_\phi\in S^{d-1}\}$
The model space $\cal K^d$
Fix $v_\phi$. A secondary circle:
$\{\cos(\theta)(v_\phi^T x)^2 + \sin(\theta)(v_\phi^T x)\mid \theta \in [0,2\pi)\}$

Note that $v_\phi$ and $-v_\phi$ share the same secondary circle.
The model space $\cal K^d$
$\mathcal{K}^d = \{ k(v_\phi, \theta; x) = \cos(\theta)(v_\phi^T x)^2 + \sin(\theta)(v_\phi^T x) \mid v_\phi\in S^{d-1}, \theta \in [0,2\pi) \}$
There is an identification $k(-v_\phi, -\theta;x) = k(v_\phi, \theta; x)$

$\mathcal{K}^2$ is a Klein bottle. $\mathcal{K}^3$ is a $3$-dimensional manifold.
The Harris Map
Harris corner/edge detector [HS 88] analyzes eigenvalues of:
$M(x) = \sum_i \Delta(x_i) \Delta(x_i)^T$, $\Delta$ finite difference gradient.
Harris map $h: x\mapsto \text{MaxEigVec}(M(x))$
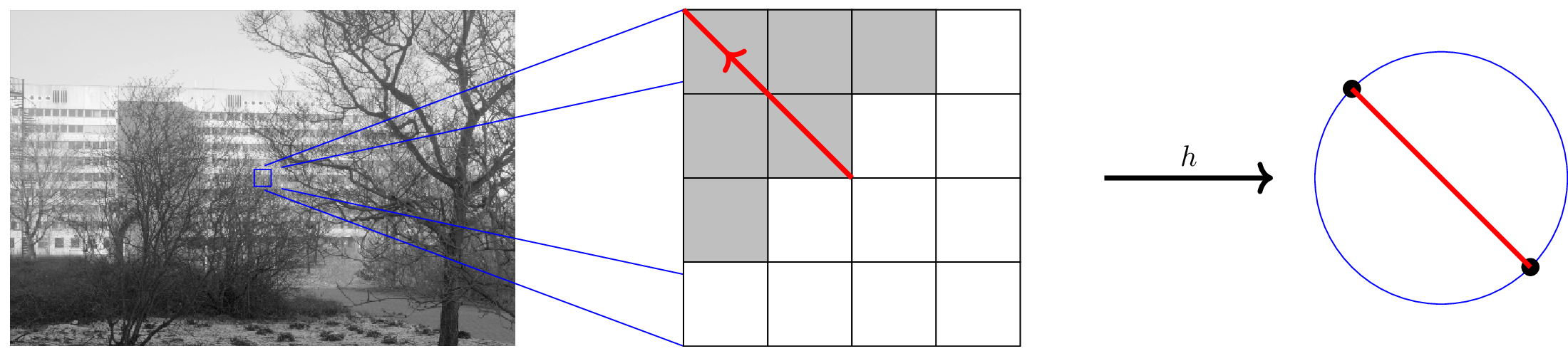
There is a sign/scale ambiguity for eigenvectors, so range is naturally $\mathbb{R}P^{d-1}$
The Harris Map
Continuous limit
$M(f(x)) = \int_x dx\, \nabla(f(x))\nabla(f(x))^T$
For $k(v_\phi, \theta; x)\in \mathcal{K}^d$, $\nabla(k(x)) = k'(x) v_\phi$
so $M(k(x))$ is rank-1, and $h(k(v_\phi, \theta; x)) = [v_\phi]$
$\mathcal{K}^d$ is a fiber bundle over $\mathbb{R}P^{d-1}$
(non-trivial because of twist in identification)
The Harris map $h$ is a fibration for $\mathcal{K}^d$
Fibers $h^{-1}([v])$ are secondary circles.
Homology of $\cal K^d$
Because of fibration structure, we can use Leray-Serre spectral sequence to compute homology.
We'll use integer ($\mathbb{Z}$) coefficients, which can be used to obtain field coefficients.
$H_\ast(\mathcal{K}^2) = (\mathbb{Z}, \mathbb{Z}\oplus \mathbb{Z}_2, 0)$
$H_\ast(\mathcal{K}^3) = (\mathbb{Z}, \mathbb{Z}_2\oplus \mathbb{Z}_2, 0, \mathbb{Z})$
BRATS patches on $\cal K^3$
 k=100, p=40: 2-sphere + circle (chord)
k=100, p=40: 2-sphere + circle (chord)
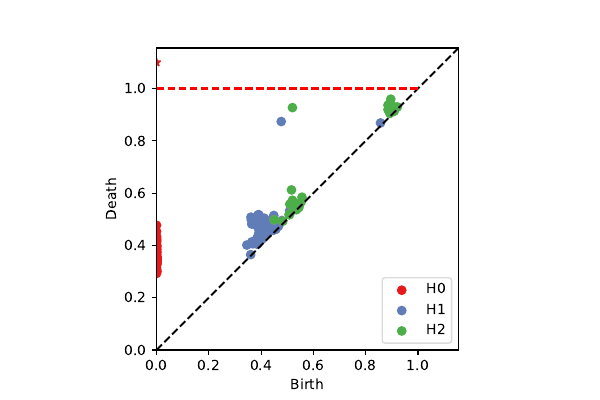 projection onto $\mathcal{K}^3$
projection onto $\mathcal{K}^3$
Penobscot patches on $\cal K^3$
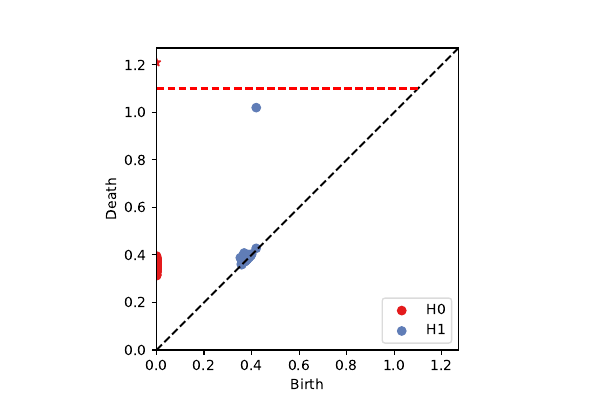 k=100, p=40: secondary circle
k=100, p=40: secondary circle
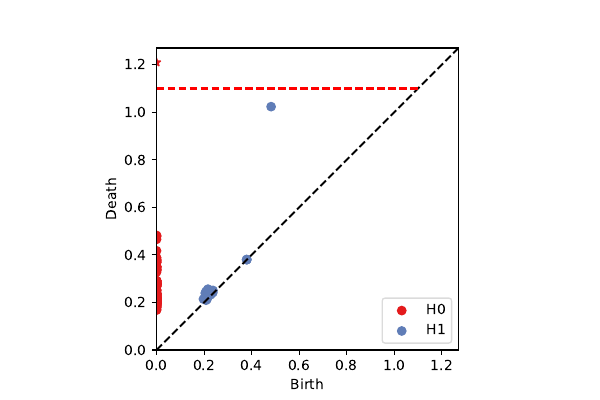 projection onto $\mathcal{K}^3$
projection onto $\mathcal{K}^3$
Review & Future Directions
We've developed a model $\cal K^d$ to explain structures we see in image patch data.
- Useful for interpreting subsets of the data.
- Captures topology of high-dimensional data with small number of dimensions.
Potential applications: 3D compression, texture, neural nets [MSC 08, PC 14, GC 19]
If we have higher-dimensional patches, we could perform similar analyses.
Where would a 4-dimensional image come from?
Other applications where we might use a map:
Evasion [AC 14],
Time series,
Control systems.
Acknowledgements
Conclusion
Review:
- New computational framework for persistent/zigzag homology.
- Parameterization by cover when building complexes.
- Parameterization of 3D patch model to understand data.
Where to next?
- We're just scratching the surface of potential "structured" methods for TDA.
- Parameterized invariants for ML pipelines?
- How can we use induced maps more effectively in TDA?
Questions?

Starters:
What are barriers to matrix factorization frameworks for other types of quiver representations?
How tight are the interleaving bounds for cover complexes?
What happens for different sized image patches?
Technical Credits
Bibliography
The contents of this talk, with complete references, can be found in:
[N 20] Bradley Nelson. Parameterized Topological Data Analysis.
Ph.D. Dissertation. Stanford University. 2020.
[AC 09] Adams, Carlsson. On the Nonlinear Statistics of Range Image Patches. 2009.
[AC 14] - Adams, Carlsson. Evasion Paths in Mobile Sensor Networks. 2015.
[BRATS] - BRATS data set. https://www.med.upenn.edu/sbia/brats2018/registration.html
[B 48] Borsuk. On the imbedding of systems of compacta in simplicial complexes. 1948.
[CWD 17] Cang, Wei, Dunbrack. TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. 2017.
[C+ 08] Carlsson, Ishkhanov, de Silva, Zomorodian. On the Local Behavior of Spaces of Natural Images. 2008.
[CDN 19] Carlsson, Dwaraknath, Nelson. Persistent and Zigzag Homology: A Matrix Factorization Viewpoint. 2019.
[CdS 10] Carlsson, de Silva. Zigzag Persistence. 2010.
[CdSM 09] Carlsson, de Silva, Morozov. Zigzag Persistent Homology and Real-valued Functions. 2009.
[CS 18] Cavanna, Sheehy. The Generlized Persistent Nerve Theorem. 2018.
[CGR 13] Chan, Carlsson, Rabadan. Topology of viral evolution. 2013.
[D 20] Dwaraknath. Quiver Theory, Zigzag Homology, and Deep Learning. 2020.
[G 72] Gabriel. Unzerlegbare Darstellungen I. 1972.
[GC 19] Gabrielsson, Carlsson. Exposition and Interpretation of the Topology of Neural Networks. 2019.
[GND+ 20] Gabrielsson, Nelson, Dwaraknath, Skraba, Carlsson, Guibas. A Topology Layer for Machine Learning. 2020.
[GGB 16] Two’s company, three (or more) is a simplex: Algebraic-topological tools for understanding higher-order structure in neural data. 2016.
[GS 17] Govc, Skraba. An Approximate Nerve Theorem. 2017.
[HS 88] Harris, Stephens. A combined corner and edge detector. 1988.
[H+ 16] Hiraoka, Nakamura, Hirata, Escolar, Matsue, Nishiura. Hierarchical structures of amorphous solids characterized by persistent homology. 2016.
[vHvdS 98] van Hateren, van der Schaaf. Independent component filters of natural images compared with simple cells in primary visual cortex. 1998.
[LPM 02] Lee, Pedersen, Mumford. The Nonlinear Statistics of High-Contrast Patches in Natural Images. 2002.
[dSC 04] de Silva, Carlsson. Topological estimation using witness complexes. 2004.
[ELZ 02] Edelsbrunner, Letscher, Zomorodian. Topological Persistence and Simplification. 2002.
[L 15] Lesnick. The Theory of the Interleaving Distance on Multidimensional Persistence Modules. 2015.
[LM 13] Lewis, Morozov. Parallel Computaiton of Persistent Homology using the Blowup Complex. 2015.
[MSC 08] Maleki, Shahram, Carlsson. A Near Optimal Coder For Image Geometry With Adaptive Partitioning. 2008.
[M] Morozov. Dionysus2. https://mrzv.org/software/dionysus2/
[M 80] Munkres. Algebraic Topology. 1980.
[N+ 20] Nguyen, Gao, Chen, Wang, Wei. Potentially highly potent drugs for 2019-nCoV. 2020.
[OS 15] Oudot, Sheehy. Zigzag Zoology: Rips Zigzags for Homology Inference. 2015.
[Pen] Penobscot Interpretation Dataset. https://zenodo.org/record/1341774
[PC 14] Perea, Carlsson. A Klein-Bottle-Based Dictionary for Texture Representation. 2014.
[R 00] Robins. Computational Topology at Multiple Resolutions: Foundations and Applications to Fractals and Dynamics. 2000.
[S 13] Sheehy. Linear-Size Approximations to the Vietoris–Rips Filtration. 2013.
[SMC 07] Singh, Memoli, Carlsson. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition. 2007.
[Y 18] Yoon. Celluar Sheaves and Cosheaves fo Distributed Topological Data Analysis. 2018.
[ZC 05] Zomorodian, Carlsson. Computing Persistent Homology. 2005.
