Parallel Computation of Zigzag Homology using Matrix Factorizations
Brad Nelson
Department of Statistics, CCAM
University of Chicago
SIAM Computational Science & Engineering
Emerging Directions in Computational Topology
March 1, 2021
bnels.github.io/cse21
Collaborators/Support

Gunnar Carlsson

Anjan Dwaraknath
Funding I received while working on this topic
- DoD through NDSEG fellowship
- DOE through SLAC/Neutrino group
- Unbox AI
Outline
- Brief introduction to Topological Data Analysis (TDA)
- Zigzag Homology
- Sequential Algorithms
- Divide and Conquer
- Experiments
Topological Data Analysis (TDA)
Concerned with understanding and using data through topology.
Data sets as topological spaces. Data points as topological spaces.
Compute algebraic signatures of shapes.
Application of homology to data begun by Robins [R 00],
furthered by [ELZ 02], [ZC 05], [CdS 10], ....
Applications (necessarily incomplete list):
Data visualization (mapper) [SMC 07], neuroscience [GGB 16], molecular properties [CWD 17], materials discovery [H+ 16], regularization [GND+ 20], genetics [CGR 13]
Topological Features
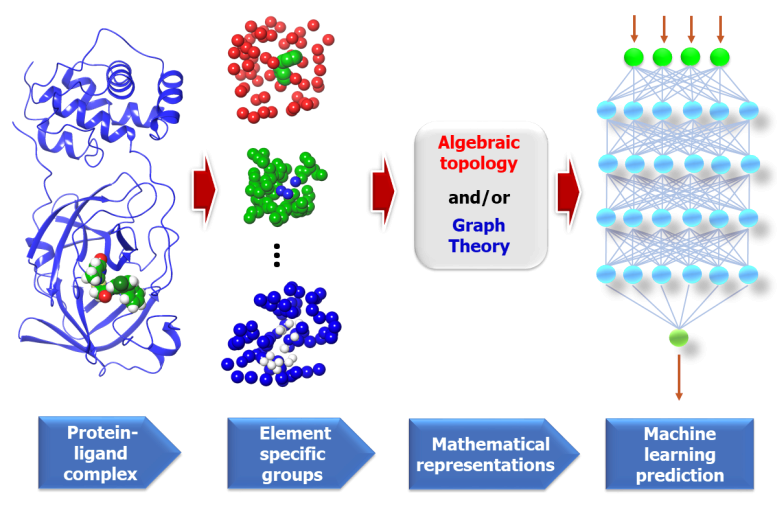
Figure from "Potentially highly potent drugs for 2019-nCoV" Nguyen et al. [N+ 20]
Topology of Data Sets

Painting by Ron Estrin
Zigzag Homology
Persistent homology [ELZ 02]
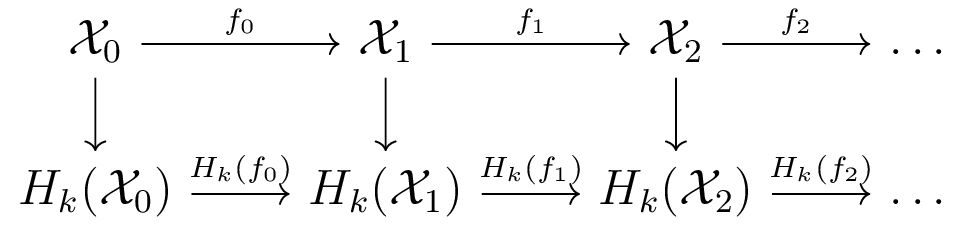
Zigzag homology [CdS 10]
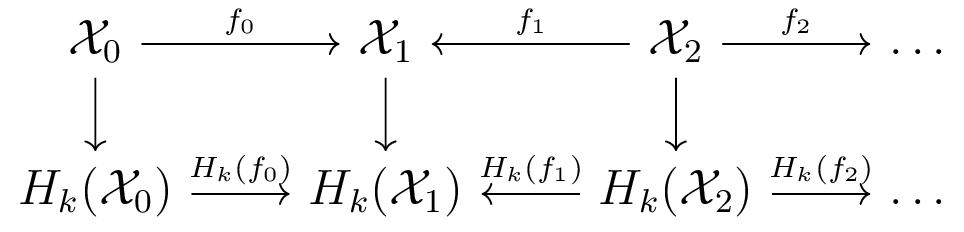
Homology turns topological spaces/maps into vector spaces/linear maps
Barcodes track how homological features appear/disappear in diagram.
Background on Zigzag Homology
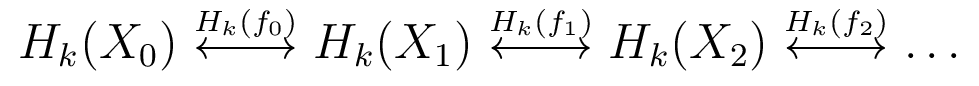
- Examples of type-A quiver representations [G 72]
- Introduced to TDA by [CdS 10]
- Algorithm for special case of inclusions [CdSM 09] implementation in Dionysus [M]
- More general version in Javaplex, used by Tausz [T 12]
- Divide and conquer approaches proposed [CdSM 09], [SVJ 12] [H 17] but no parallel implementations.
- Other work on zigzag, e.g. [OS 15] [O 15] [MO 14] [MS 19]
Contributions
- New computational framework for computing zigzag homology
- Handles arbitrary maps between spaces
- Parallel implementation using OpenMP
Persistent and Zigzag Homology: A Matrix Factorization Viewpoint [CDN 19+]
Code: github.com/bnels/BATS and github.com/bnels/BATS.py
Parallelization of Homology Functor
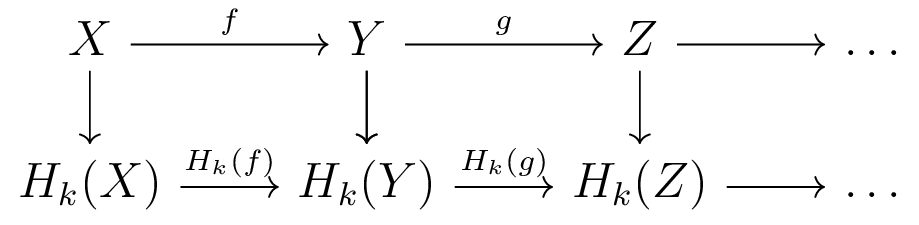
- Computing Homology of each space embarassingly parallel
- Computing each induced map embarassingly parallel
Many existing TDA packages work on filtered chain complexes
(sensible if all maps are inclusions)
We take advantage of this parallelization.
The Companion Matrix
Put diagram of induced maps on homology into matrix with block adjacency structure.
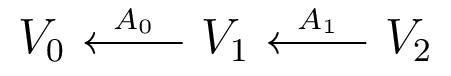
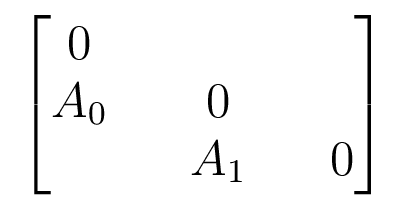
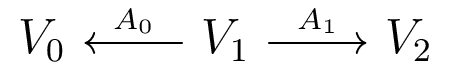
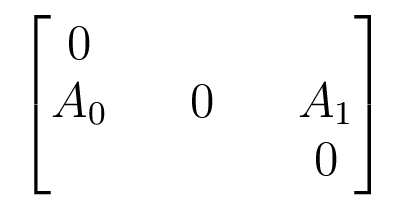
Acts on $V_0 \oplus V_1 \oplus V_2$
The Barcode Factorization

$E_i$ have at most 1 nonzero in each row and column
Can read barcode off from $\Lambda$ by tracking basis vectors
[CDN 19+]: the barcode form $\Lambda$ exists and uniquely determines isomorphism class (following [G 72])
Righward-Initial Algorithm
Building Blocks:- Matrix factorizations $A = LE_L UP$ and $A = PU\hat{E}_L L$
- Variants of LU decomposition with different loop orders/pivot strategies
- $E_L$ matrices have structure so $E_L L = \tilde{L}E_L$ (shape commutation)
- $\hat{E}_L$ matrices have structure so $L \hat{E}_L = \hat{E}_L \tilde{L}$ (shape commutation)
- Lower/upper triangular matrices closed under multiplication, inversion.
Sequential Algorithm

Leftward-Initial Algorithm
- Use two new factorizations: $A = PLE_U U$ and $A = U \hat{E}_U LP$
- $E_U$ matrices have structure so $U E_U = E_U \tilde{U}$ (shape commutation)
- $\hat{E}_U$ matrices have structure so $\hat{E}_U U = \tilde{U}\hat{E}_U$ (shape commutation)
- Start on other end of quiver, similar game
Divide-and-Conquer
- We can start the leftward and rightward algorithms in parallel
- At some point in the first pass, the algorithms meet on an edge
- Depending on edge direction, use $A = LQU$ factorization or $A = UQL$
- $Q$ is in pivot form. Commute $L$ matrix to start, $U$ matrix to end
- Can cheaply convert to leftward or rightward form by propoagating permutations
- Can use this recursively in parallel
Parallel Performance
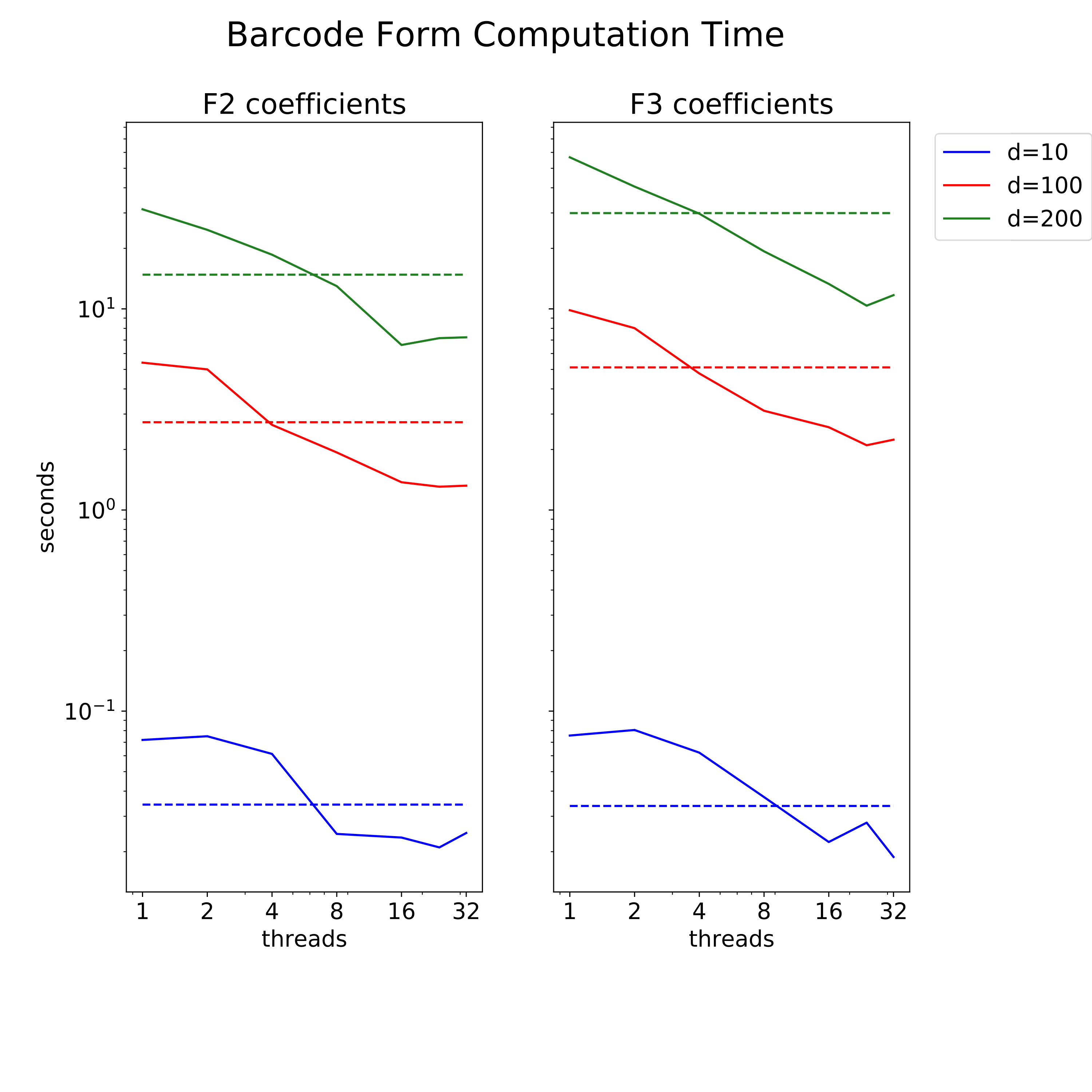
Parallel speedup of divide and conquer algorithm
$d$ - vector space dimension
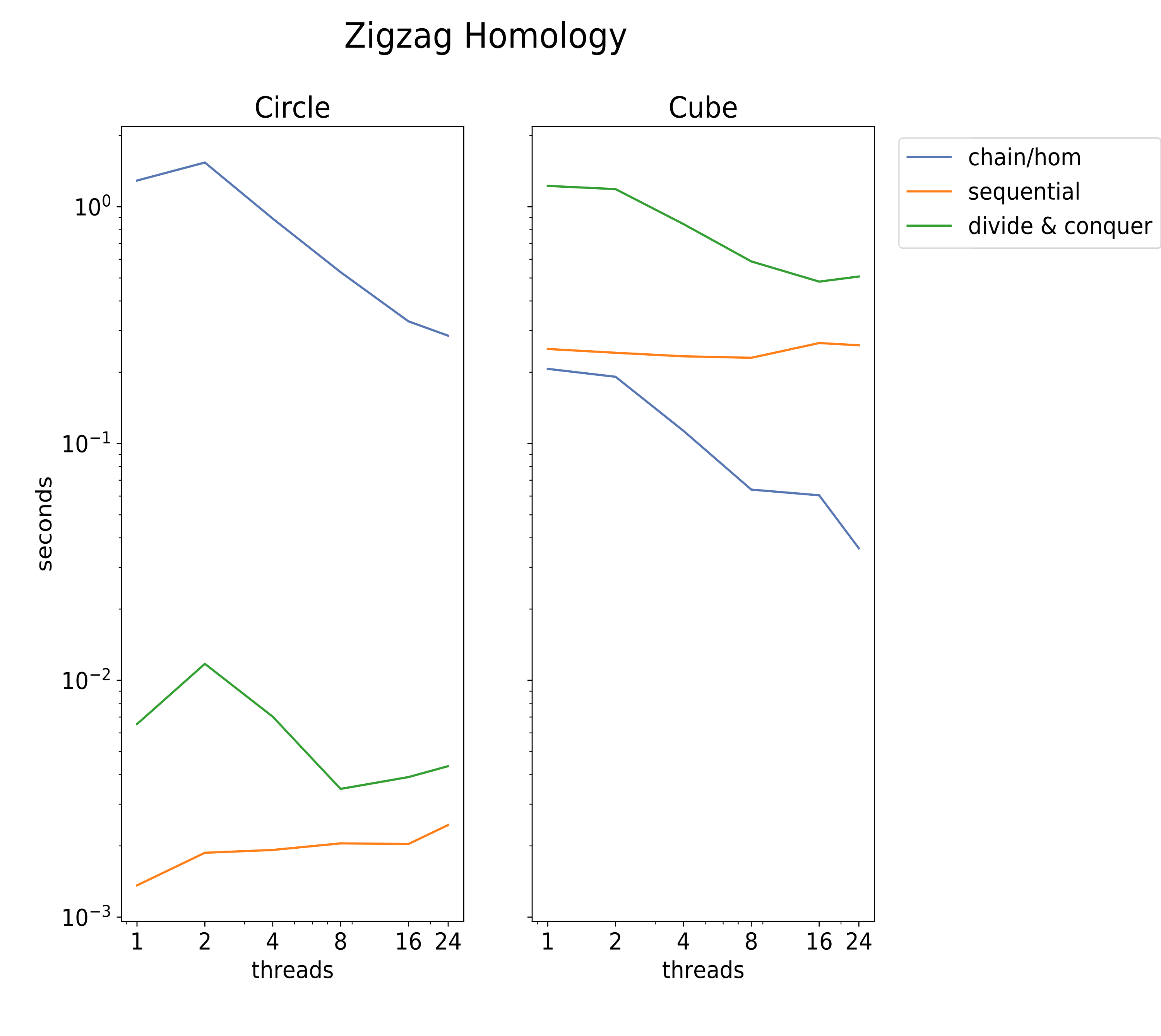
Parallel speedup of full zigzag homology.
Left: large chain complex, small homological dimension.
Right: small chain complex, large homological dimension.
Comparison vs Dionysus
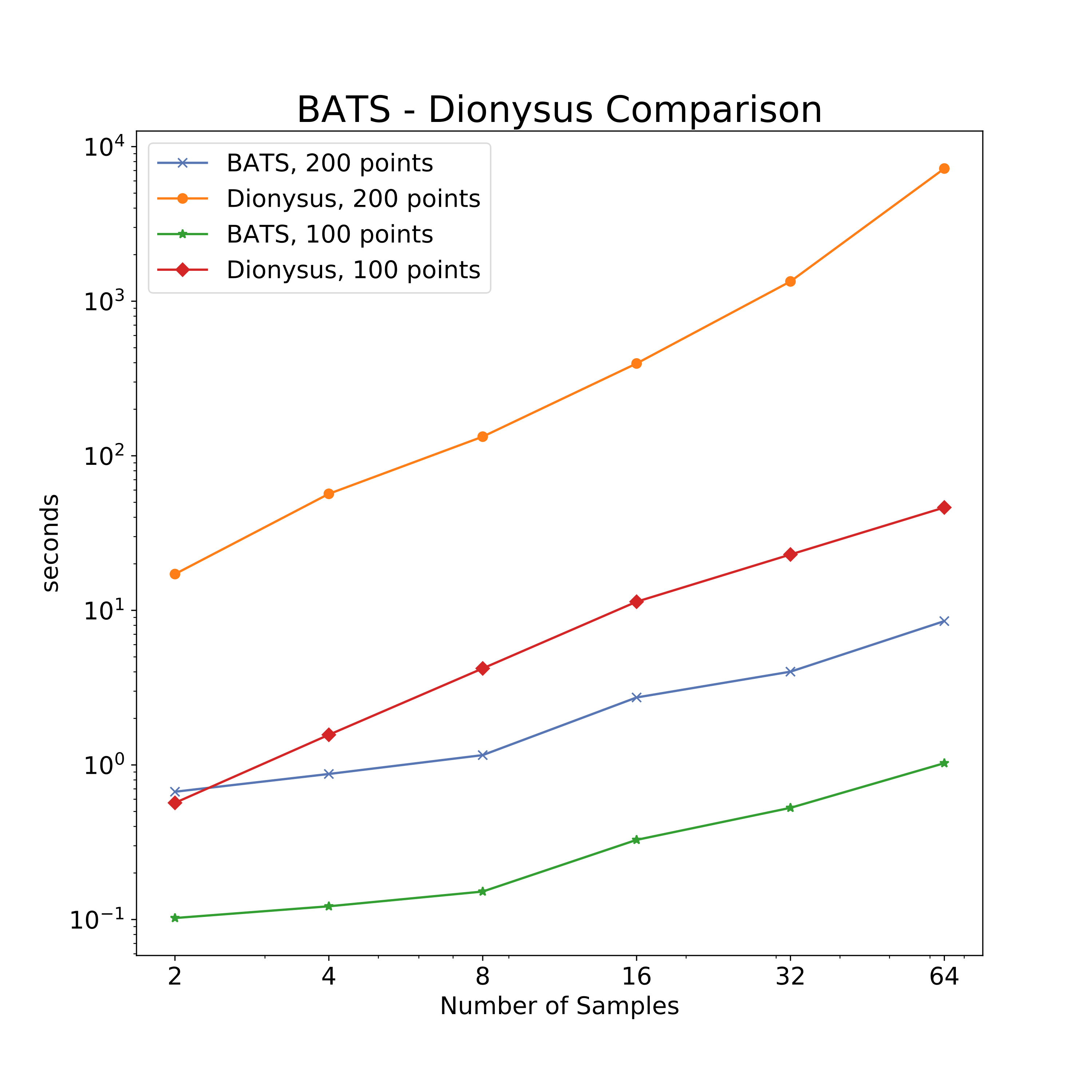
"Topolgical bootstrapping" samples from circle.
Morozov Zigzag
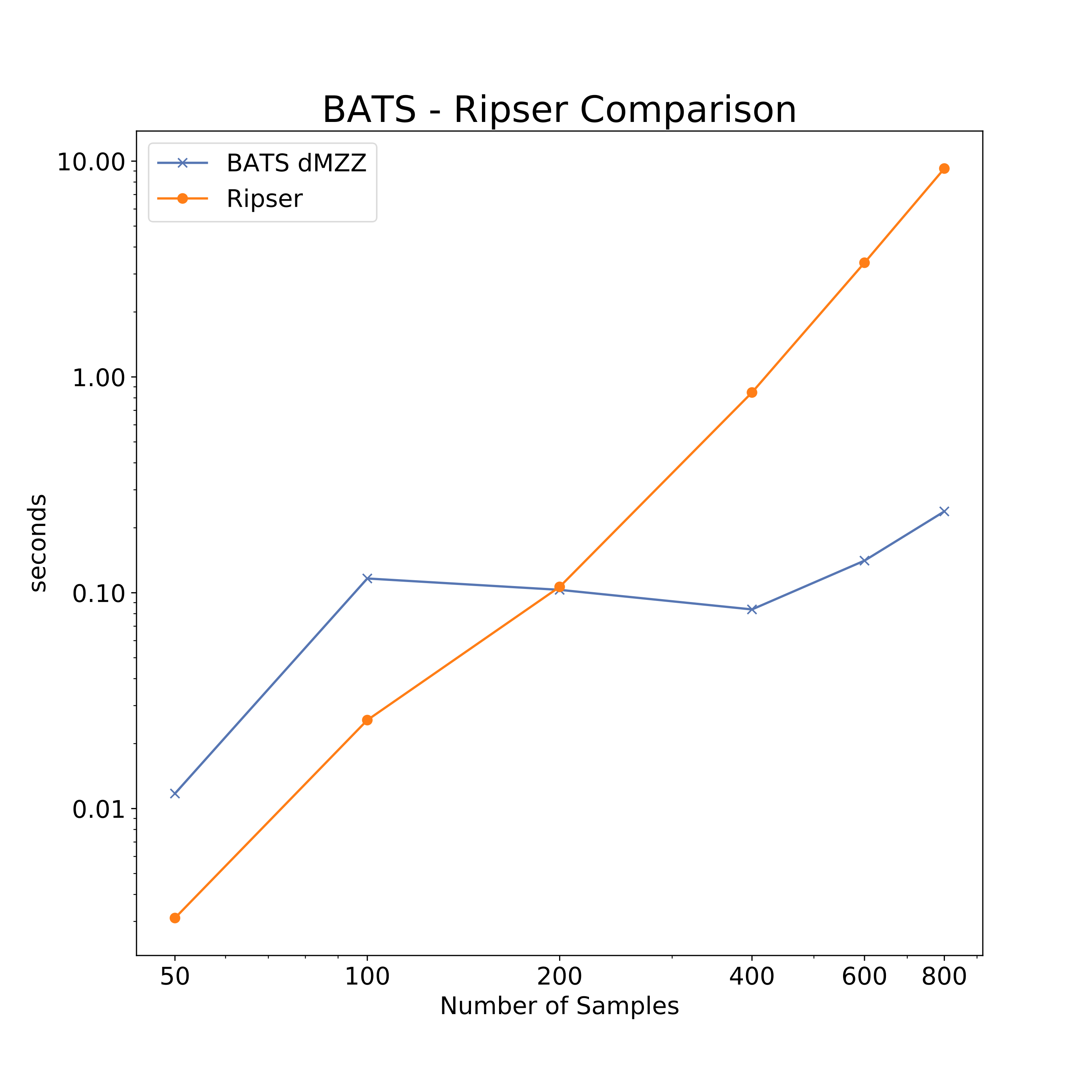
Discrete Morozov zigzag on circle using parameters from [OS 15]. Ripser does full PH computation.
Review and Future Directions
- Matrix factorization framework for zigzag homology.
- Can be applied to any maps.
- Fully parallel implementation.
Future directions:
- Combine with other optimizations for (persistent) homology.
- Extend support for zigzag applications.
Questions?
Technical Credits
Bibliography
The contents of this talk, with complete references, can be found in:
[CDN 19+] Carlsson, Dwaraknath, Nelson. Persistent and Zigzag Homology: A Matrix Factorization Viewpoint. (Sumbitted)
https://arxiv.org/abs/1911.10693
[C+ 08] Carlsson, Ishkhanov, de Silva, Zomorodian. On the Local Behavior of Spaces of Natural Images. 2008.
[CDN 19+] Carlsson, Dwaraknath, Nelson. Persistent and Zigzag Homology: A Matrix Factorization Viewpoint. 2019.
[CdS 10] Carlsson, de Silva. Zigzag Persistence. 2010.
[CdSM 09] Carlsson, de Silva, Morozov. Zigzag Persistent Homology and Real-valued Functions. 2009.
[CGR 13] Chan, Carlsson, Rabadan. Topology of viral evolution. 2013.
[G 72] Gabriel. Unzerlegbare Darstellungen I. 1972.
[GND+ 20] Gabrielsson, Nelson, Dwaraknath, Skraba, Carlsson, Guibas. A Topology Layer for Machine Learning. 2020.
[GGB 16] Two’s company, three (or more) is a simplex: Algebraic-topological tools for understanding higher-order structure in neural data. 2016.
[H 17] Henselman. Talk at the SIAM minisymposium in Applied and Computational Topology. 2017.
[H+ 16] Hiraoka, Nakamura, Hirata, Escolar, Matsue, Nishiura. Hierarchical structures of amorphous solids characterized by persistent homology. 2016.
[ELZ 02] Edelsbrunner, Letscher, Zomorodian. Topological Persistence and Simplification. 2002.
[MO 14] Maria, Oudot. Zigzag persistence via reflections and transpositions. 2014.
[MS 19] Maria, Schreiber. Discrete morse theory for computing zigzag persistence. 2019.
[M] Morozov. Dionysus2. https://mrzv.org/software/dionysus2/
[N+ 20] Nguyen, Gao, Chen, Wang, Wei. Potentially highly potent drugs for 2019-nCoV. 2020.
[O 15] Oudot. Persistence Theory: From Quiver Representations to Data Analysis. 2015.
[OS 15] Oudot, Sheehy. Zigzag Zoology: Rips Zigzags for Homology Inference. 2015.
[R 00] Robins. Computational Topology at Multiple Resolutions: Foundations and Applications to Fractals and Dynamics. 2000.
[SMC 07] Singh, Memoli, Carlsson. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition. 2007.
[SVJ 12] Skraba, Vejdemo-Johansson. Parallel & scalable zig-zag persistent homology. 2012.
[T 12] Tausz. Extensions and applications of persistence based algorithms in computationaltopology. 2012.
[ZC 05] Zomorodian, Carlsson. Computing Persistent Homology. 2005.