Topological Data Analysis,
Linear Algebra, and Optimization
Brad Nelson
CCAM, Department of Statistics
University of Chicago
November 5, 2020
bnels.github.io/cam-intro
Collaborators/Support
Collaborators who appear in this work
- Gunnar Carlsson
- Anjan Dwaraknath
- Rickard Bruel-Gabrielsson
- Primoz Skraba
- Leonidas Guibas
Funding I received while working on these topics
- DoD through NDSEG fellowship
- DOE through SLAC/Neutrino group
- Unbox AI
Outline
- Introduction to Topological Data Analysis (TDA)
- Matrix factorization algorithms for TDA
- Topology for Optimization
Topological Data Analysis (TDA)

Topological Data Analysis (TDA)
Concerned with understanding and using data through topology.
Data sets as topological spaces. Data points as topological spaces.
Compute algebraic signatures of shapes.
Application of homology to data begun by Robins [R 00],
furthered by [ELZ 02], [ZC 05], [CdS 10].
Applications (necessarily incomplete list):
Data visualization (mapper) [SMC 07], neuroscience [GGB 16], molecular properties [CWD 17], materials discovery [H+ 16], regularization [GND+ 20], genetics [CGR 13]
Topological Features
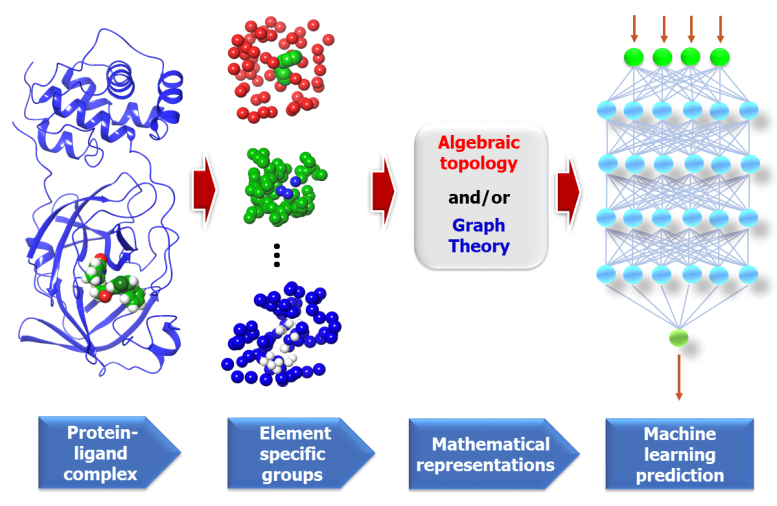
Figure from "Potentially highly potent drugs for 2019-nCoV" Nguyen et al. [N+ 20]
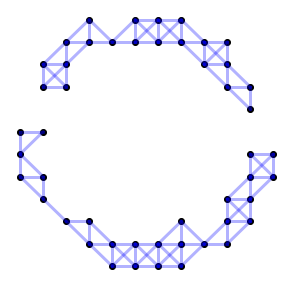
Topology of Data Sets

Homology
Homology turns statements about topology into statements about linear algebra.
- Topological spaces $X$ have associated vector spaces $H_k(X)$
- Continuous maps $f:X \to Y$ have associated linear maps $F_k: H_k(X) \to H_k(Y)$
The index k refers to the dimension of topological features.
- $\dim H_0(X)$ is the number of connected components.
- $\dim H_1(X)$ is the number of loops/holes.
- $\dim H_k(X)$ is the number $k$-dimensional voids.
- $F_k:H_k(X) \to H_k(Y)$ tells us how features in $X$ map to features in $Y$
Persistent and Zigzag Homology
Persistent homology [ELZ 02]
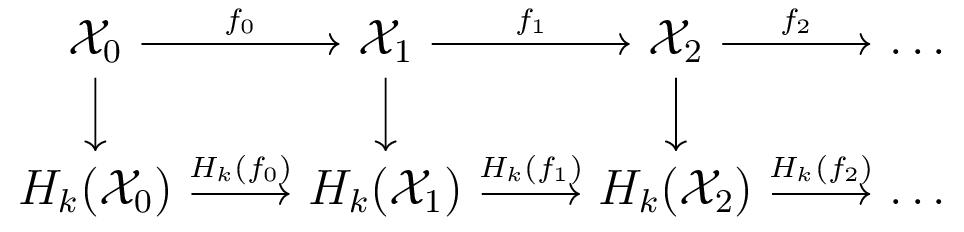
Zigzag homology [CdS 10]
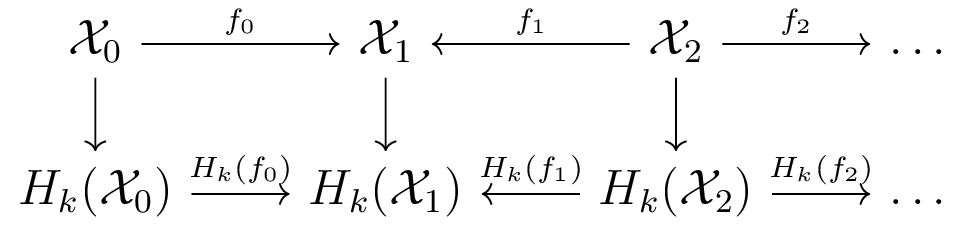
Barcodes track how homology is created and destroyed.
Computing Zigzag Homology
How can we compare two (or more) samples?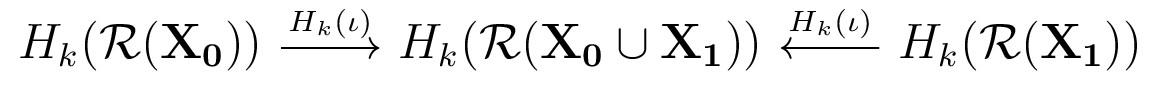
Topologically, look at maps to union.
Something like this proposed in [CdS 10]: "Topological bootstrapping"
Prior Work on Zigzag Homology
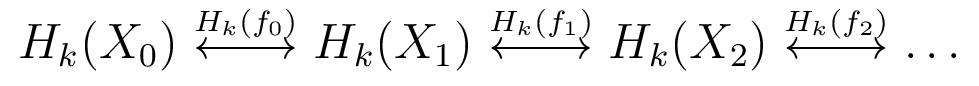 Note: persistent homology is special case
Note: persistent homology is special case
- Zigzag homology introduced by [CdS 10]
- Algorithm for special case of inclusions [CdSM 09]
- Only widely available implementation in Dionysus [M]
- Work on applications to Rips complexes [OS 15]
- Examples of type-A quiver representations [G 72]
Applications limited by slow computations
Contributions
- New computational framework for computing persistent and zigzag homology
- Handles larger classes of problems
- Multiple opportunities for parallelization
- Orders of magnitude faster than existing implementations.
Persistent and Zigzag Homology: A Matrix Factorization Viewpoint [CDN 19]
Code: BATS and BATS.py
Parallelization of Homology Functor
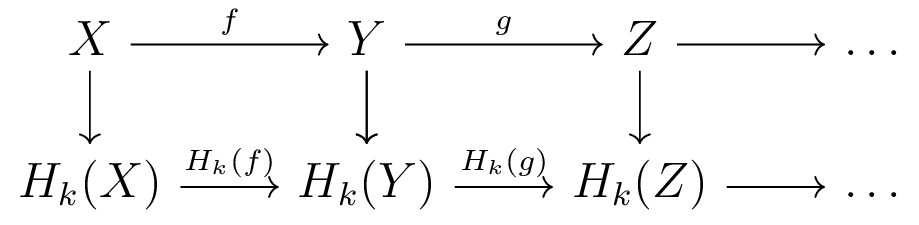
- Computing Homology of each space embarassingly parallel
- Computing each induced map embarassingly parallel
Existing TDA packages work on chain complexes
(Makes sense in certain situations)
We take advantage of this parallelization.
Quiver Representations
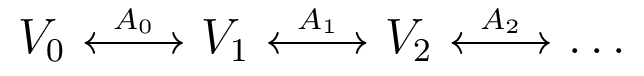
- Diagram of vector spaces, linear transformations
- type-A quiver representations are on a line graph
- [G 72]: type-A quiver representations have finite indecomposables
- [CdS 10]: barcodes are the indecomposable forms
Example: Indecomposable for bar with birth at 1, death at 2:
$I[1,2] = 0 \leftrightarrow \mathbb{F} \overset{\cong}\leftrightarrow \mathbb{F} \leftrightarrow 0 \leftrightarrow \dots$
Type-A quiver representations are isomorphic to something in the form
$\bigoplus_i I[b_i, d_i]$
These are Jordan 0 blocks in the case where all arrows go the same direction. [H 17]
The Companion Matrix
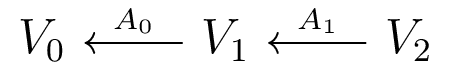
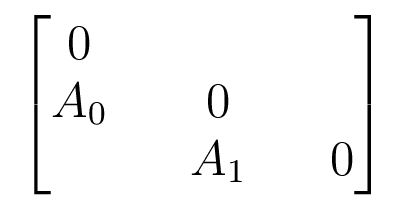
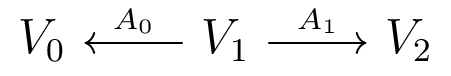
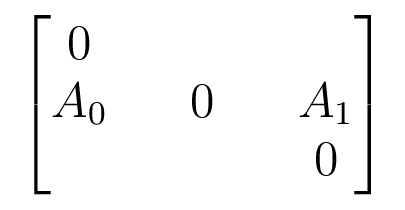
Block matrix with structure of adjacency matrix of underlying graph.
Acts on $V_0 \oplus V_1 \oplus V_2$
The Barcode Factorization

$E_i$ have at most 1 nonzero in each row and column
Can read barcode off from $\Lambda$ by tracking basis vectors
[CDN 19]: the barcode form $\Lambda$ doesn't depend on choice of basis in each vector space
Further Details
- Reversed arrows use different factorization ($PU\hat{E}_L L$).
- Can start at other end of diagram using another set of factorizations ($PLE_U U$).
- Combine to get divide-and-conquer scheme to parallelize.
- General algorithm uses 6 variations of the LU decomposition.
The game: you can commute $L$ matrices with $E_L$ and $\hat{E}_L$ in certain ways.
You can commute $U$ matrices with $E_U$ and $\hat{E}_U$ in certain ways.
Choose factorizations accordingly.
Complexity
- Parallel homology calculation: $O(m_i^3)$ ($m_i$ max number simplices on node)
- $n$ edges in the quiver, maximum vector space dimension $d$.
- Proposition: the sequential algorithm runs in $O(nd^3)$ time.
- Proposition: the parallel divide-and conquer algorithm runs in $O((d \log d) n + d^3 \log n)$ time.
- Regular zigzag homology: $\tilde{O}(m^\omega)$ ($m$ total number simplices) [MMS 11]
Sparsity makes all these bounds pessimistic in practice.
Performance
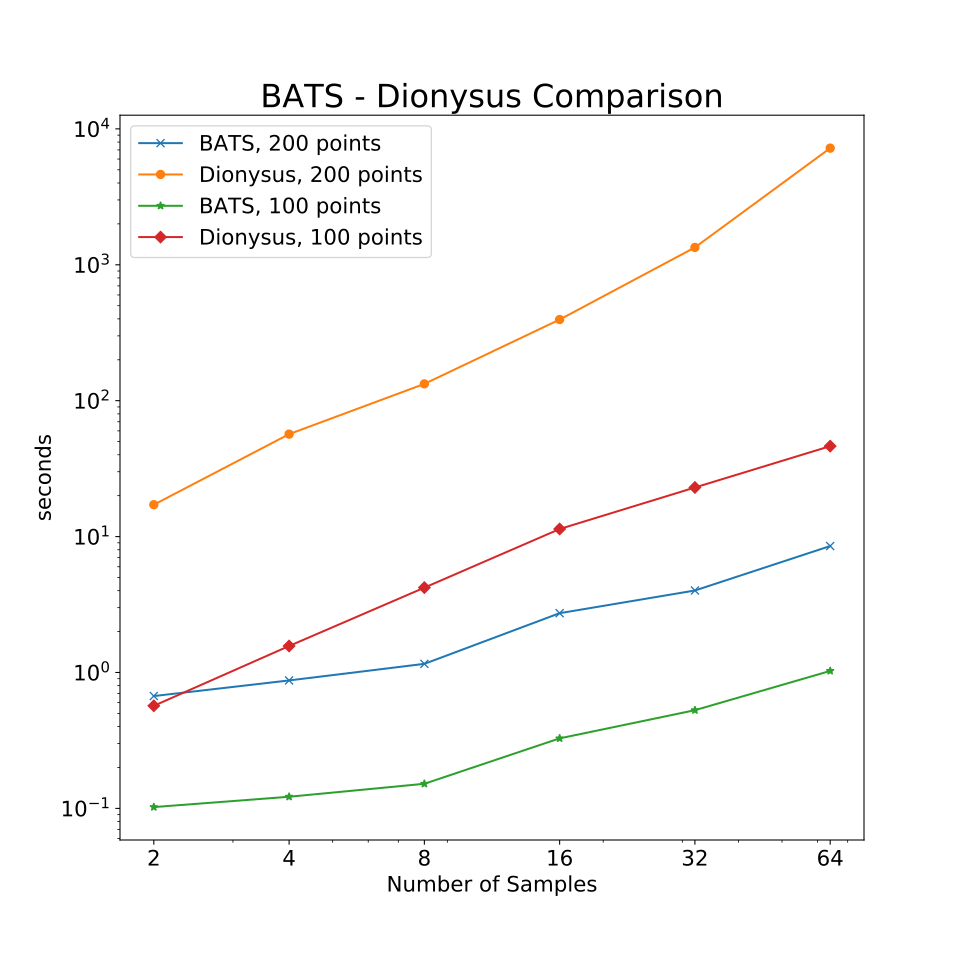
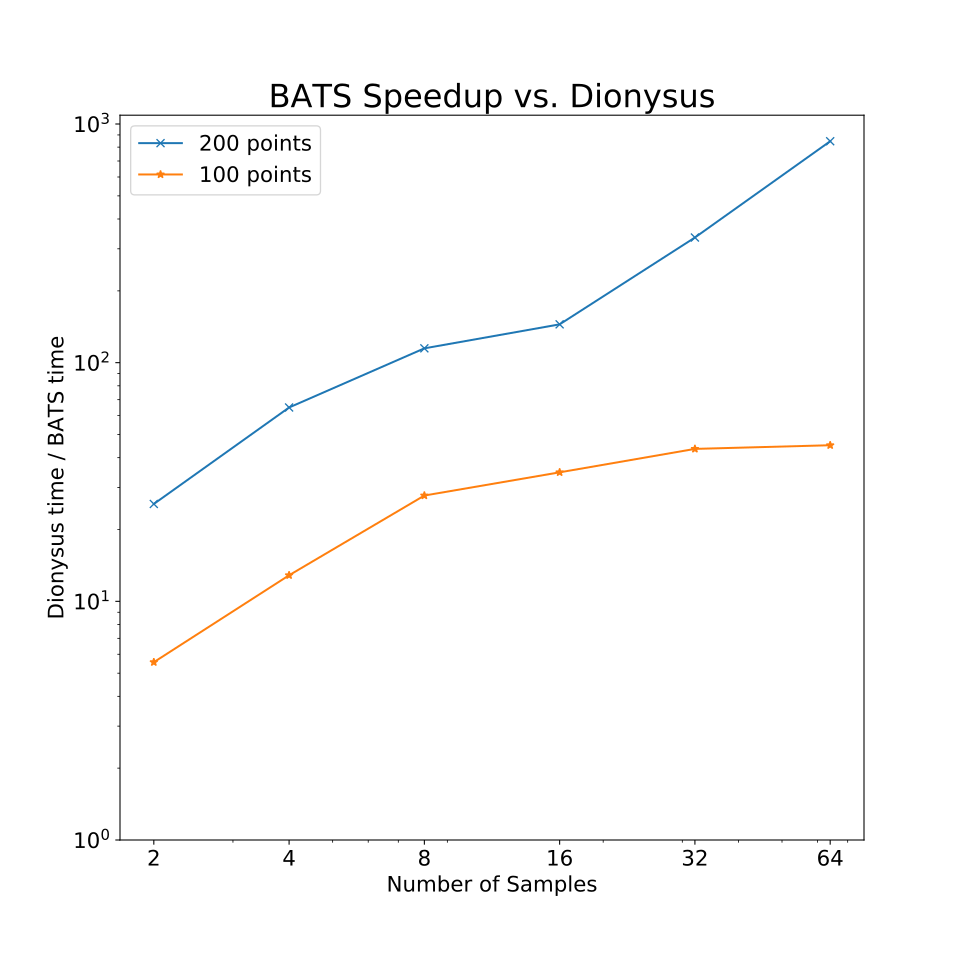
Performance vs. Dionysus [M] on zigzag of samples
Parallel Performance
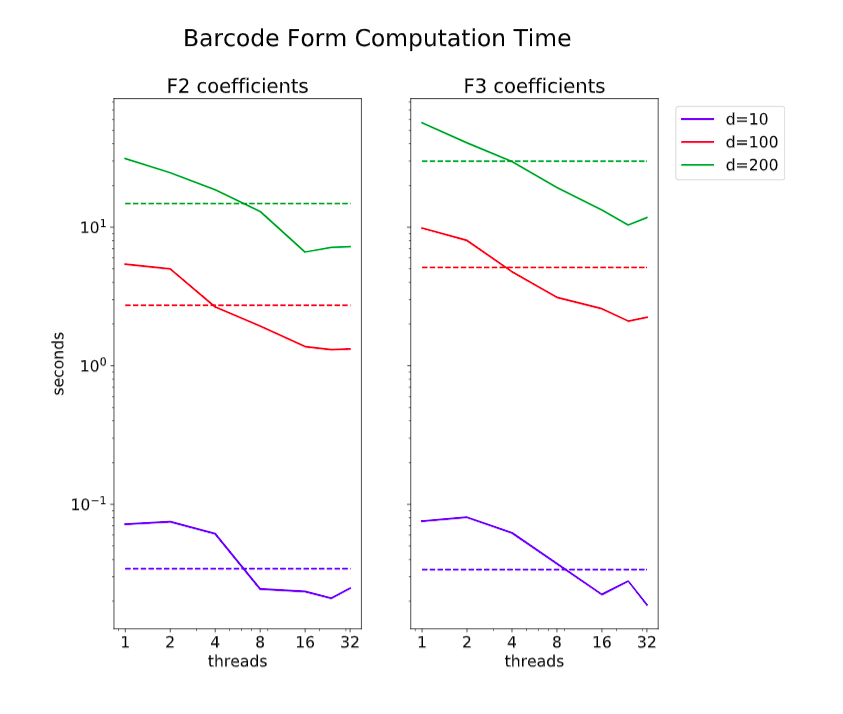
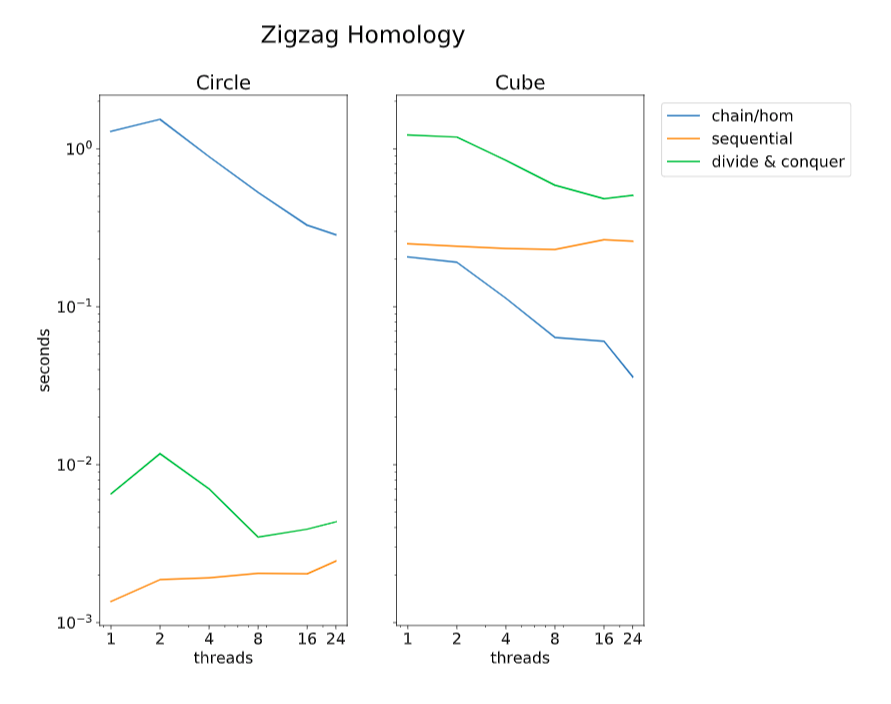
Left: Parallel speedup of divide-and-conquer algorithm.
Right: breakdown of computation time for full problem.
Review and Future Directions
- Matrix factorization framework for persistent/zigzag homology.
- Can be applied to any maps.
- New applications possible (not covered here).
Future directions:
- Quiver representations other than type-A?
- Combine with other optimizations for persistent homology.
Persistent Homology and Optimization
"A Topology Layer for Machine Learning" (AISTATS 2020) [GND+ 20]
PyTorch extension: TopologyLayer
Sampling of other recent work in this area:
- Use of topological features in deep learning (Hofer et al. 2017).
- Topological shape matching (Poulenard et al. 2018).
- Regularization for tumor segmentation (Clough et al. 2019).
- Regularization of decision boundaries (Chen et al. 2019).
Our contributions
- General purpose implementation for using PH in gradient-based optimization.
- Several new examples, including adversarial attacks.
Topological Failures of Neural Networks


Left: the digit "4". Right: digits dreamed by a GAN. What's wrong?
Level Set Filtrations



Top: Image. Bottom: Level sets as simplicial complexes, filtered by pixel intensity.
Mapping Barcodes to Functions
Lemma (trivial): Every simplex addition either creates homology or destroys homology.
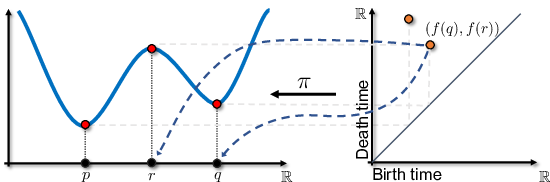
Implication: We can map the birth and death times of particular homology classes back to function values at particular points.
Generally, compute a sub-gradient of loss with respect to filtration value.
Functions of Barcodes
We consider simple algebraic functions of barcodes. Others are possible.
$$\{(b_i, d_i)\} \mapsto \sum_i (d_i - b_i)^p (b_i + d_i)^q$$ We can choose $p, q$ to measure desired topological behavior.
- $p = 2, q=0$ is large if there are very persistent classes ($H_0$: well-separated clusters, $H_1$: large holes)
- $p = 0, q=1$ measures the mid-point of bars in the filtration.
Topologically Penalized GAN
Idea: penalize GANs for unnatural topology.
We want one connected component, so penalize sum of lengths of $H_0$ bars.

Setup for training GAN with topological loss.
Topologically Penalized GAN



Left: under-trained GAN.
Center: improve for 50 batch iterations with topology loss.
Right: improve for 60k batch iterations.
Point Cloud Optimization





Clockwise from top center: Uniformly distributed points. Decrease $H_0$. Decrease $H_1$. Increase $H_1$ + decrease $H_0$. Increase $H_1$. Increase $H_0$.
Adversarial Attacks


Left: Image of the digit "4". Right: An adversarial attack to misclassify as "8".
Conclusion
Review:
- New computational framework for persistent/zigzag homology.
- Parallel algorithms, and fast implementation.
- Optimization using persistent homology in penalty.
Where to next?
- Algorithms for other quiver types?
- Topology-constrained dimension reduction?
- Topological summaries/control of neural networks?
Winter Quarter: STAT 37411 = CAAM 37411 Topological Data Analysis
Technical Credits
Bibliography
[CWD 17] Cang, Wei, Dunbrack. TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. 2017.
[C+ 08] Carlsson, Ishkhanov, de Silva, Zomorodian. On the Local Behavior of Spaces of Natural Images. 2008.
[CDN 19] Carlsson, Dwaraknath, Nelson. Persistent and Zigzag Homology: A Matrix Factorization Viewpoint. 2019.
[CdS 10] Carlsson, de Silva. Zigzag Persistence. 2010.
[CdSM 09] Carlsson, de Silva, Morozov. Zigzag Persistent Homology and Real-valued Functions. 2009.
[CGR 13] Chan, Carlsson, Rabadan. Topology of viral evolution. 2013.
[D 20] Dwaraknath. Quiver Theory, Zigzag Homology, and Deep Learning. 2020.
[G 72] Gabriel. Unzerlegbare Darstellungen I. 1972.
[GC 19] Gabrielsson, Carlsson. Exposition and Interpretation of the Topology of Neural Networks. 2019.
[GND+ 20] Gabrielsson, Nelson, Dwaraknath, Skraba, Carlsson, Guibas. A Topology Layer for Machine Learning. 2020.
[GGB 16] Two’s company, three (or more) is a simplex: Algebraic-topological tools for understanding higher-order structure in neural data. 2016.
[H 17] Henselman, Gregory. Matroids and Canonical Forms: Theory and Applications. Ph.D. Dissertation. University of Pennsylvania. 2017.
[H+ 16] Hiraoka, Nakamura, Hirata, Escolar, Matsue, Nishiura. Hierarchical structures of amorphous solids characterized by persistent homology. 2016.
[dSC 04] de Silva, Carlsson. Topological estimation using witness complexes. 2004.
[ELZ 02] Edelsbrunner, Letscher, Zomorodian. Topological Persistence and Simplification. 2002.
[LM 13] Lewis, Morozov. Parallel Computaiton of Persistent Homology using the Blowup Complex. 2015.
[MMS 11] Milosavljevic, Morozov, Skraba. Zigzag Persistent Homology in Matrix Multiplication Time. 2011.
[M] Morozov. Dionysus2. https://mrzv.org/software/dionysus2/
[M 80] Munkres. Algebraic Topology. 1980.
[N+ 20] Nguyen, Gao, Chen, Wang, Wei. Potentially highly potent drugs for 2019-nCoV. 2020.
[OS 15] Oudot, Sheehy. Zigzag Zoology: Rips Zigzags for Homology Inference. 2015.
[PC 14] Perea, Carlsson. A Klein-Bottle-Based Dictionary for Texture Representation. 2014.
[R 00] Robins. Computational Topology at Multiple Resolutions: Foundations and Applications to Fractals and Dynamics. 2000.
[S 13] Sheehy. Linear-Size Approximations to the Vietoris–Rips Filtration. 2013.
[SMC 07] Singh, Memoli, Carlsson. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition. 2007.
[ZC 05] Zomorodian, Carlsson. Computing Persistent Homology. 2005.